Uniform Curvature Combs on Cross Sections
One great feature of Alias is the ability to display a curvature comb on visual cross sections. How a curvature comb varies over a cross section curve tells a lot about the structure of the surface. Unfortunately, in versions of Alias before 2011, curvature combs on cross sections did not look so great. For example, here's one from Alias 2010.
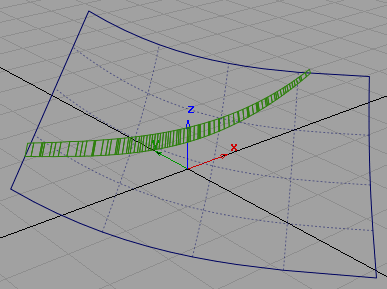
So why does it look like this? Well, to find out, let's turn on the tesselation and zoom in.
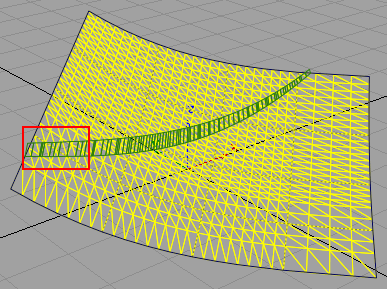

Notice that the sample points for both the section curve and its curvature comb all occur on edges of the tessellation's triangles. This indicates that rather than doing a true intersection between the NURBS surface and the cross section plane, the section curve is calculated by doing a triangle-plane intersection with the cross section plane and each triangle in the tessellation.
There is one compelling reason for why visual sections are generated this way: speed. Even with an extremely dense tessellation, it is still significantly faster to compute many triangle-plane intersections than do one full NURBS-plane intersection. Furthermore, it is very straightforward to parallelize such an algorithm to take advantage of multiple cores. The tradeoff is that the section curve you get is only an approximation whose accuracy depends on the density of the tessellation. However, this is acceptable for visual sections since they are not meant for engineering purposes, but rather to understand the structure of the surface while interactively modeling.
Unfortunately, though the approach is fast, visual quality suffers since there is no association between the tessellation and the cross section plane. That said, here is what visual sections look like in Alias 2011:

OK, so besides the new colour scheme, notice that the samples are uniformly spaced. Looks nicer, yes? So what did we do?
Recall that the original algorithm was based on computing a triangle-plane intersection for each triangle in the tesselation. The result of that intersection was a line segment which was then sent to the draw system to be rasterized. As far as the draw system is concerned, it receives a stream of these line segments and it just has to show them on the screen. It turns out that those little line segments all connect together to make the section curves, but they may not be emitted in order.
For Alias 2011, rather than direct each line segment to the draw system, we instead direct them to a data structure that allows them to be efficiently connected. After connecting them, we have a polyline representation that can easily be uniformly resampled with the number of samples specified by the user. The additional time taken by these two steps is dependent on the number of cross section curves, though on average a 10% overhead was measured (compared to Alias 2010). That said, performance is still interactive and this slowdown is not noticeable even on large models.
Just like in Alias 2010, the new technique calculates the curvature values along the section curve by barycentrically interpolating the coefficients of the second fundamental form which were evaluated at the vertices of the original tessellation. Also like Alias 2010, the fidelity of the section curve is directly related to the density of the surface's tessellation.